 .
.
Para trazar la gráfica de una función de dos variables, en el espacio tridimensional, es de mucha ayuda construir un mapa compuesto por un conjunto de curvas, que permiten imaginar de alguna manera, la superficie.
| Curvas de nivel |
 .
.
Para trazar
la gráfica de una función de dos variables, en el espacio
tridimensional, es de mucha ayuda construir un mapa compuesto por un conjunto
de curvas, que permiten imaginar de alguna manera, la superficie.
| Definición. | Sea
z=f(x,
y), y sea k una constante real perteneciente al recorrido de
f.
El conjunto
de todos los puntos (x, y) del plano XY tales que f(x,
y)=k, se denomina
curva de nivel de la superficie z=f(x,
y) en k.
|
| . | |
| Notación. | Denotando por Nk(f) a la curva de nivel de f en k, se tiene: |
|
|
|
| . | |
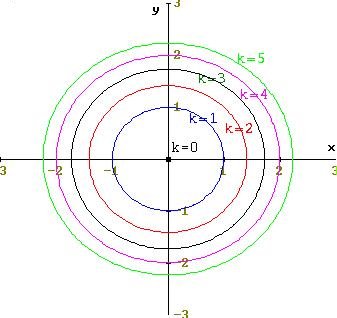
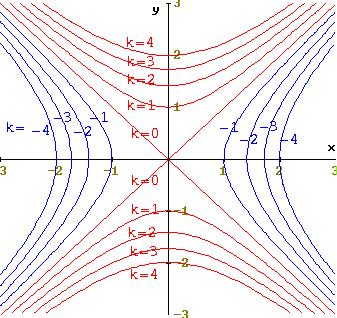
| Nota. | Para
cada k en el recorrido de f, existe la curva
de nivel Nk(f)
generándose una familia de curvas de nivel de la función f |
.
|
 |
|
 |
|
|
 |
 |
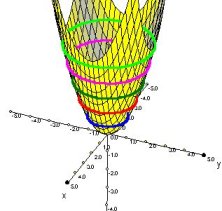 |
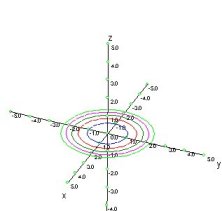
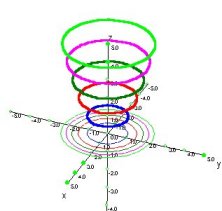
Ejemplos de Gráficos
de superficies y curvas de nivel
|
|
|
|
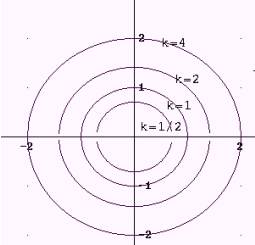 |
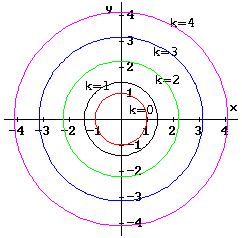
Paraboloide elíptico:
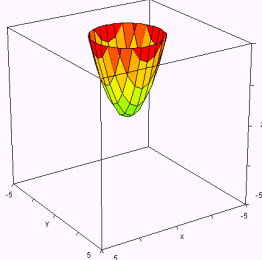 |
|
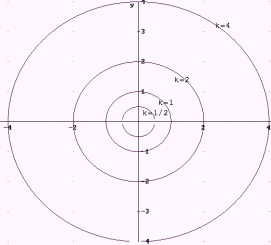 |
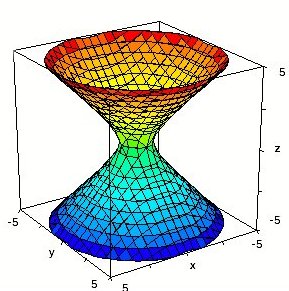
Superficie cónica
(de una hoja): 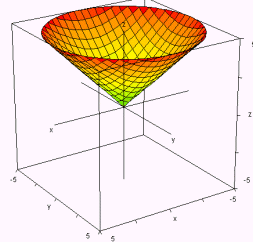 |
|
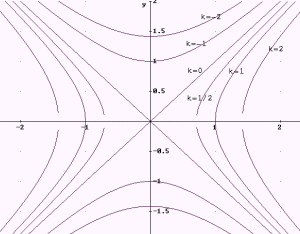 |
Paraboloide hiperbólico z = x2 - y2 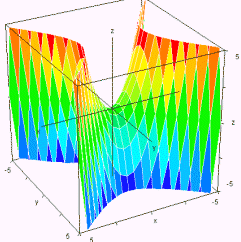 |
|
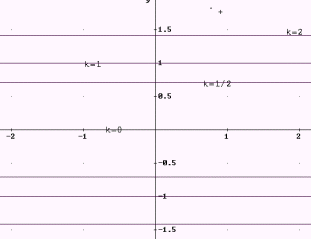 |
Superficie cilíndrica y = x2 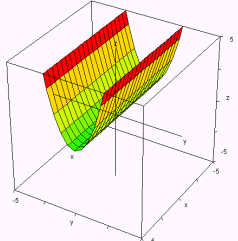 |
|
 |
 |
|
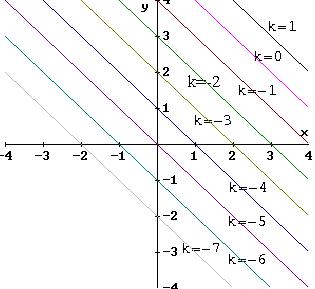 |
Plano z = x+y-5 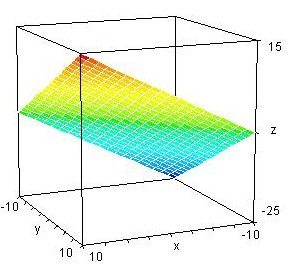 |
|
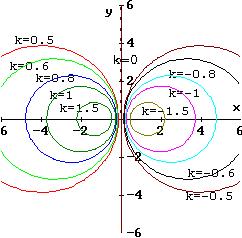 |
Superficie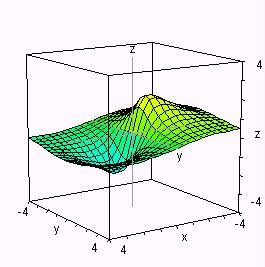 |
Ejemplos de Gráficos de superficies y curvas de nivel (animaciones)
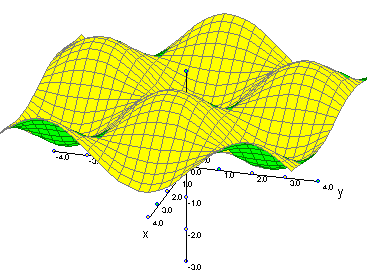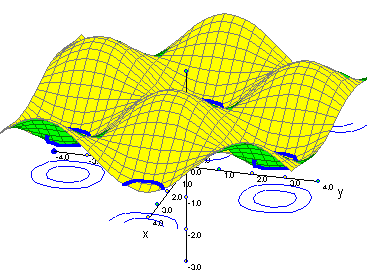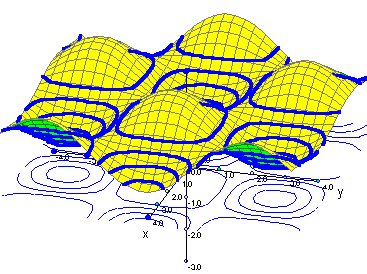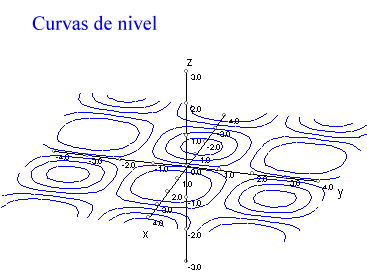
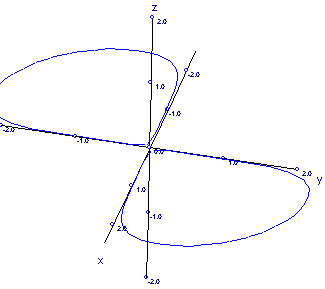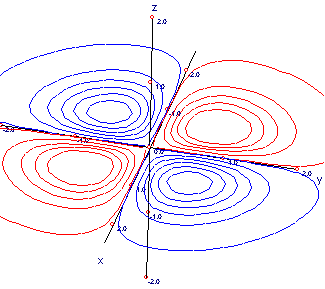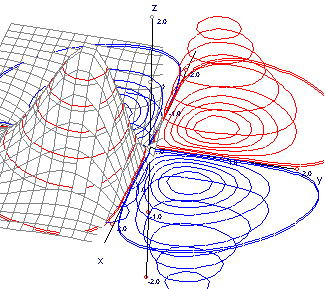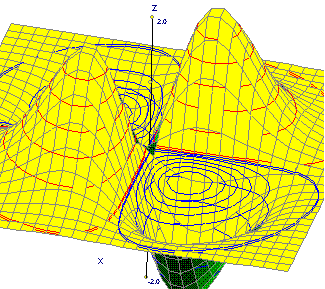
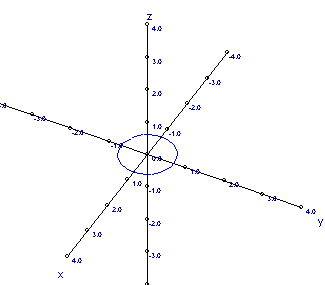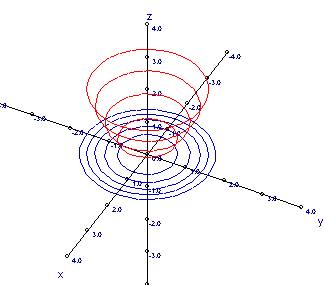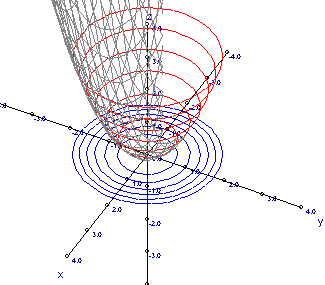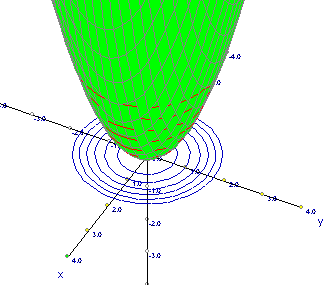
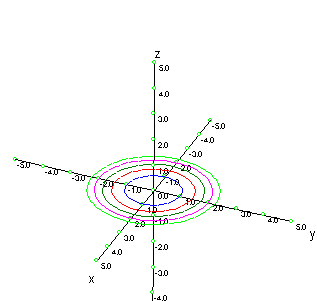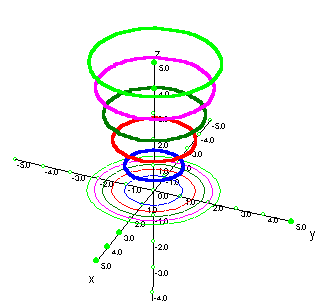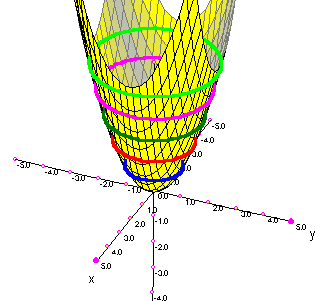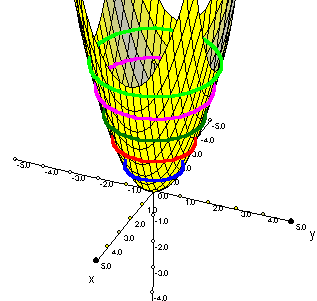
Curvas de nivel de:
| Un cerro |
 |
| Un cráter |
 |
| Una loma |
 |
| Nota. | El trazado de las curvas de nivel se constituye en un método para graficar funciones de dos variables. Muchos software computacionales utilizan este método para graficar superficies. |
Funciones de tres variables.
Para funciones de tres variables, el conjunto solución de la ecuación u=f(x, y, z) es subconjunto de IR4.
Se puede tener
una idea de algún comportamiento de una función de tres variables,
determinando y analizando las supeficies de nivel, que se definen
de manera equivalente a la curvas de nivel.
| Definición. | Las
superficies de nivelde u=f(x, y, z)
son superficies
del espacio IR3
cuyas ecuaciones son de la forma f(x, y, z) = k siendo k una constante real, perteneciente al recorrido de f |
|
Universidad de Talca |
||
|
Instituto de Matemática y Física |