| ¿Conoce este método para
resolver una ecuación cuadrática?: |
| |
-
Un video |
| |
-
Artículo:
A Simple Proof of the Quadratic
Formula Po-Shen Loh
|
|
|
Temas a trabajar: |
| |
-
Definición de Polinomios con coeficientes en un
cuerpo. . .. |
| |
* Grado de un polinomio |
| |
* Igualdad de polinomios. |
| |
-
Anillo de polinomios. |
| |
-
Anillo de división (cuerpo no conmutativo) |
| |
-
Algoritmo de división. |
| |
Ejercicio: Efectuar la
división
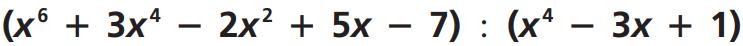 |
| |
-
Teorema del resto. |
| |
-
Raíces y factorización de polinomios |
| |
-
División sintética |
| |
-
Teorema fundamental del álgebra. Factorización
(en diferenres cuerpos: Q, IR, C) |
| |
-
Raíces de polinomios con coeficientes enteros. |
| |
-
Estudio gráfico de Funciones polinomiales y
racionales |
| |
*
Gráficas de Funciones Polinómicas
(LibreTexts) |
| |
*
Funciones racionales (LibreText) |
| |
|
|
| |
-
Aplicaciones: |
| |
-
Modelos de ajuste e interpolación lineal y no
lineal (polinomios de Lagrange) |
| |
*
Interpolación |
| |
|
|
Referencias |
| |
-
Polinomios
Pablo De
Nápoli
-
Polinomios Heraldo González Serrano
-
Polinomios (Matemática general) Daniel
Jiménez B. |
| |
|
| |
|
|
Tarea (22/08/23): |
| |
|
1) |
Determinar los
valores de a y b en el polinomio p(x)=2x3-5x2+ax+b,
sabiendo que p(x) es divisible por x2-4 |
|
|
|
|
2)
|
Determinar los
valores de k de modo que el polinomio
p(x)=2x3 - 4x + 3k cumpla,
por separado, las siguientes condiciones. |
| |
a) Tiene como
factor a q(x)=x+3 |
| |
b) Al
dividirlo por (x+2) se obtiene resto 5 |
| |
c) Es
divisible por (x+1) |
| |
d) Tiene como
raíz al 4 |
| |
e) Es igual al
polinomio s(x)=2(x32x+7) |
|
|
|
|
3)
|
Operatoria de
polinomios en un software (adición,
sustracción, producto y división).
Comandos y ejemplos. |
|
|
|
|
|
|
Mini-investigaciónes: |
|
1) |
Estudiar si existe un
algoritmo equivalente a la división sintética,
que permita multiplicar de manera más rápida
un polinomio p(x) por (x+a). Este algoritmo se
debería llamar multiplicación sintética.
|
|
2) |
Cómo usted sabe el método
de división sintética permite dividir, de manera
más rápida, un polinomio por (x-a). Estudiar si
es posible ajustar el método de división
sintetica para dividir por un polinomio del tipo
(px-a) |
| |
Evaluación: 1 punto
en la Prueba 1 del curso (solo al primer
alumno que resuelva exitosamente esta mini-investigación). |
| |
|
|
Buscando todas
raíces de un polinomio...que no siempre se
encuentran |
|
 |
|
A continuación se
comentas los pasos a seguir para
encontrar (cuando se pueda) todas las
raíces de un polinomio p(x).
|
| |
|
1) |
Raíces nulas |
| |
Separar las raíces
nulas de p(x), en caso que éstas existan |
| |
|
|
2)
|
Número posible de
raínes positivas y negativas |
| |
Usar la Regla de
los signos de Decartes, para establecer
como se pueden distribuir las raíces
entre posibles raíces positivas,
negativas y complejas. |
| |
|
|
3) |
Raíces racionales |
| |
Buscar las raíces
racionales de p(x), aplicando el
criterio correspondiente. Como se sabe,
en caso que p(x) no tenga raíces
racionales, la aplicación de este método
será tiempo perdido. |
| |
|
|
4) |
Raíces complejas |
| |
Tener presente que
si sabe que un complejo a+bi es raíz de
p(x), entonces a-bi tambien es una raíz. |
| |
|
|
5) |
Teorema del factor |
| |
Cada vez que
encuentre una raíz x0, usando
el teorema del factor, p(x)=(x-x0)q(x)
y seguir trabajando con q(x) |
| |
|
|
6) |
Raíces múltiples |
| |
Cada vez que
encuentre una raíz x0,
revisar si ella se repite (una vez, o más)
como raíz de p(x). |
| |
|
| |
Revisar
ejemplos aquí:
Técnicas elementales para buscar raíces |
| |
|
| |
Actividades
 |
| |
y comprobar sus resultados con un
software adecuado. |
| |
|
|
Estudio gráfico de Funciones polinomiales y
racionales |
| |
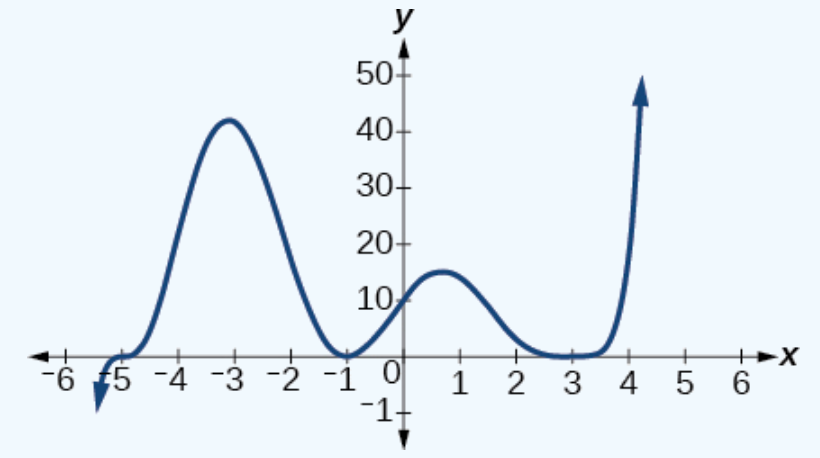
Gráfica de una
función polinómica con grado 5. |
| |
*
Gráficas de Funciones Polinómicas
(LibreTexts) |
| |
*
Funciones racionales (LibreText) |
| |
|
|