Programación Lineal
Método punto de esquina.
Con las inecuaciones se nos pueden presentar
problemas de la vida cotidiana. En este caso trabajaremos con problemas de solo
2 incógnitas, en la cual vamos a optimizar (maximizar y minimizar).
Los pasos a seguir son:
1. F(x,y) à Función objetivo
2. Leer
3. Plantear sistema
4. Resolver
5. Región poligonal
6. Vértices à solución à optimice F(x,y)
Problema
Una máquina produce
dos tipos de televisores, A y B. Para fabricarlos se necesita un tiempo de
producción en máquinas y un acabado a mano que realizan los operarios.
* La venta del modelo
A necesita 2 horas en la máquina y 1/2 hora de trabajo a mano, produce un
beneficio de $60.000.
* La venta del modelo
B necesita 3 horas en la máquina y 1/4 horas de trabajo a mano, produce un
beneficio de $55.000.
Se dispone
un total de 300 horas de
trabajo en máquinas y 60 horas de
trabajo a mano. Entre los dos tipos de zapatos han de fabricarse por lo menos 90. ¿Qué cantidad de televisores de
cada tipo se debe producir para lograr que el beneficio sea máximo?
Solución:
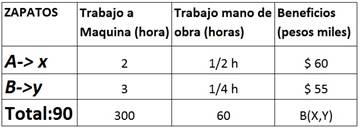
Primer paso: Ordenar los datos
en una tabla como la que ven a continuación. Se debe identificar correctamente
las variables “X” e “Y”, de estas sale la utilidad ($80.000 y $60.000)
Para identificar las
variables debemos leer muy bien el problema
* *
1.- Ahora, procedemos a hacer la
Función que representa este problema, como tenemos que ver el beneficio
llamaremos a la función B(x,y),
para hacer la función debemos ver los beneficios que producen las ventas de los
televisores de tipo X y de tipo Y, entonces la función quería así:
B(x,y)= 60x + 55y ß Función objetivo
![]() 3.- Plantearemos el sistema de
inecuaciones:
3.- Plantearemos el sistema de
inecuaciones:
·
Este es
nuestro sistema de inecuaciones
En este caso, primero veremos la inecuación para el trabajo a
máquina: 2x + 3y ≤ 300
·
Y luego, escribimos la inecuación para el trabajo a
mano: ½ x + ¼ y ≤
60
·
Entre ambos televisores debemos producir como mínimo
90: x +
y ≥ 90
·
Y las condiciones obvias, no se puede producir
negativo por tanto: x , y ≥ 0
![]()
Cada una de estas
inecuaciones representa (sin el signo >= ó <=) una línea recta, por
tanto, las representaremos en un plano:
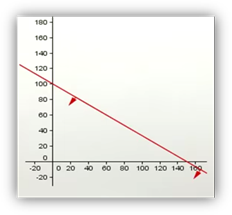
Luego tomamos los puntos (0,0) y los reemplazamos en
la función, y nos queda que cero es menor
o igual a 300
Por tanto la recta apunta hacia los puntos (0,0). Y
así lo hacemos con las 2 rectas restantes hasta quedarnos algo como esto:


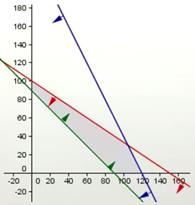

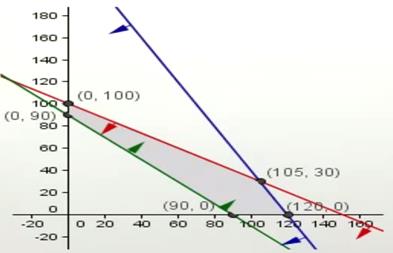
Función Beneficio:
B(x,y)= 60x + 55y
B(0,90)=
4.950.000
B(0,100)=
5.500.000
B(90,0)=
5.400.000
B(120,0)=
7.200.000
B(105,30) = 7.950.000
Respuesta: Para maximizar el beneficio debemos
fabricar 105 televisores del tipo A y 30 del tipo B
Bibliografía:
Gráficos y problema tomados de https://www.youtube.com/watch?v=wsywXvBMjso
Libro: Colección Matemáticas para la Administración,
Algebra Lineal y Métodos Cuantitativos -- Carlos Mario Morales C
Hecho por Marcelo Arce C. y Franco Figueroa F. de la
carrera Ing. Informática Empresarial de la Universidad de Talca, Chile.

