 TALLER
DE MATEMÁTICAS
TALLER
DE MATEMÁTICASPuedes mandarnos tus soluciones, sugerencias,
problemas, curiosidades matemáticas....
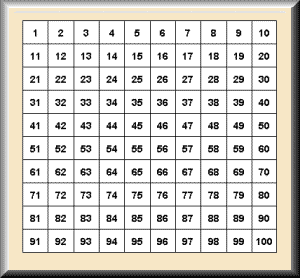
Cada equipo alternativamente lanza un dado 4 veces y anota los resultados.
Cada equipo tacha todos los números del tablero que haya podido obtener enlazando los números obtenidos mediante 3 operaciones ( se puede utilizar +, -, · , ÷ )
Por ejemplo, si han salido 3, 3, 2, 5 se pueden tachar los siguientes números
(3 · 3) + (2 · 5) = 19
(3 + 3 + 2) · 5 = 40
(3 · 5) - (3 · 2) = 9
(3 · 2 · 5) : 3 = 10
(5 - 2) · 3 · 3 = 27
Gana el equipo que ha tachado más números.
En un tablero de 4X4 casillas se escriben 16 números enteros de 2 cifras.
Por ejemplo
| 8 | 35 | 16 | 6 |
| 15 | 14 | 20 | 11 |
| 9 | 40 | 12 | 29 |
| 18 | 35 | 50 | 24 |
En este caso tacharía del tablero el número 24 de la esquina inferior derecha
Reglas del juego:
Número de jugadores (2 o 3)
1. Se echa a suertes para ver que jugador comienza.
2. Cada jugador, por orden, lanza los tres dados ( o un dado tres veces ) y obtiene tres números.
3. Con esos números realiza dos operaciones aritméticas ( -, +, · . ÷ ) o elevar un número a otro, o extraer raíces, en las que índice y radicando son dos de los tres números obtenidos pudiendo repetir operación, apuntando en un papel las operaciones realizadas para que las vea el contrario y tacha el número de la tabla obtenido.
4. Si un jugador, con los números obtenidos no puede tachar ninguno de los números libres del tablero, pasa el turno al siguiente jugador.
5. Si un jugador no ha obtenido ningún número de la tabla por no haber encontrado las operaciones convenientes, tacha el número el primer jugador que descubra la combinación adecuada
6. La partida termina cuando todos los números de la tabla estén tachados
7. Gana el jugador que ha tachado más números.
Este problema es en apariencia sencillo, sin embargo no es tan simple y, para resolverlo vamos a tener que recurrir a algunas estrategias de resolución de problemas.
Para abordarlo es conveniente que:
a) dibujes un diagrama de la
situación. No es tan fácil.
b) inténtalo utilizando
un tubo cilíndrico y un hilo.
La superficie dibujada no se parece a ninguna de las formas planas cuya área conoces.
ESTRATEGIA: Imagínate un problema parecido pero
más sencillo
Cambia el corral circular por uno cuadrado del mismo
perímetro.
Ahora el problema es bastante más sencillo.
Dibuja un diagrama de la situación actual.
Observa que las regiones que se forman son sectores
circulares cuyos radios y amplitudes respectivas puedes deducir
facílmente.
Cambia el cuadrado por un octógono y repite
el proceso
¿Qué edad tiene Alfredo? y ¿yo?
Sugerencia: lee con atención, piensa en la diferencia
de edad entre ambos y en que los años
pasan para los dos igual. Utiliza ecuaciones si te
hace falta.
2. Tres amigos tienen 21 botes de coca-cola, 7 de ellos están llenos, 7 vacíos y 7 llenos hasta la mitad exactamente. ¿Cómo deben repartirse los botes para que los tres se lleven el mismo número de botes y la misma cantidad de coca-cola? ( No se puede trasvasar de un bote a otro)
3. ¿Cómo te las ingeniarías para
cortar en 8 trozos iguales un disco de papel, dando sólo tres cortes
rectos?
2. ¿Cuántas veces a lo largo de un día las agujas de un reloj forman un ángulo recto?
3. Tres cervezas, 7 refrescos y una ración de calamares
cuestan 2800 pts; 4 cervezas, 10 refrescos y una ración cuestan
3400 pts. ¿Cuánto habrá que pagar por una cerveza,
un refresco y una ración?
En un campo la hierba crece en todas partes con igual rapidez y espesura. Sa sabe que 70 vacas se la comerían en 24 días y 30 vacas en 60 días. ¿Cuántas vacas serían necesarias para comerse toda la hierba en 96 días?
2. Una brigada está formada por 6 armadores y un carpintero. Cada armador gana 20.000 ptas y el carpintero 3.000 ptas más que el salario medio de los miembros de la brigada incluído el mismo. ¿Cuánto ganaba el carpintero?
3. Un coche va por una carrtera a velocidad constante.
En un momento dado pasa por delante de un poste kilométrico que
tiene un número de dos cifras. Al cabo de una hora pasa por delante
de otro poste que curiosamente tiene las mismas dos cifras pero en oden
inverso.
Su sorpresa es enorme cuando al acbo de otra hora pasa
por otro poste que lleva las mismas cifras separadas por un cero. ¿A
qué velocidad va el coche?

Eres el piloto de una avioneta que
es capaz de viajar a una velocidad de 300 km/h sin viento.Tienes
combustible para 4 horas de vuelo. Despegas del aeropuerto y en el viaje
de ida tienes un viento a favor de 50 km/h,
lo que eleva tu velocidad hasta 350 km/h. De repente te
das cuenta de que en el viaje de vuelta tendrás el viento en contra
y volarás a 250 km/h.
Puedes ayudarte de una gráfica
que muestre cómo varía la distancia al aeropuerto en función
del tiempo para calcular la máxima distancia
a la que puedes llegar.
Primer
dado: 1 1 2 2 3 3
Segundo
1 1 1 2 2 2
Tercero
0 0 1 1 2 2
Encuentra las siguientes probabilidades:
a) que los tres dados den un número
par
b) que los tres tengan el mismo
número
c) que la suma de los tres dados
sea par