Presentación.

  Todo el mundo conoce a Pitágoras aunque sólo sea por el teorema que lleva su nombre.

 
" El área cuadrado construido sobre la hipotenusa de un triángulo rectángulo es igual a la suma de las áreas de los cuadrados construidos sobre los dos catetos".
 
 

Antes de profundizar en este teorema por qué no investigamos algo acerca de Pitágoras y de su época.

¿Quién era?, ¿dónde y cuándo vivió?, ¿qué culturas le influyeron?, ¿qué era la escuela pitagórica?, ¿cómo estaban organizados?, ¿que Matemáticas utilizaron?, ¿que otros descubrimientos hicieron?, ¿cuáles han llegado hasta nosotros?, ¿cómo y para qué los utilizamos?....

Como veremos investigar sobre todos estos interrogantes nos va a permitir no sólo entender un poco
más del mundo clásico sino desarrollar e investigar sobre un buen número de contenidos del
curriculum de este curso distribuidos en varios bloques: Números, Álgebra, Geometría, Azar... Pero
vamos a desarrollar no sólo contenidos conceptuales sino también procedimentales y actitudinales...
 

Actividad previa:

El profesor guiará y orientará esta búsqueda de información, proporcionando materiales fotocopiados,
seleccionando textos e ilustraciones - sería conveniente contar con la colaboración del departamento
de Cultura Clásica y de Música del centro - . Se puede utilizar en esta fase el vídeo Donald en el país
de las Matemáticas.

Una vez explorados y contextualizados los conocimientos matemáticos más característicos de la
escuela pitagórica se seleccionan uno o dos más asequibles al desarrollo cognitivo de los alumnos.

Sugerimos estos dos:

     1. Números poligonales.

     2. La sección aurea.

Realizamos una propuesta detallada del desarrollo de uno de ellos.

1. Números poligonales

Se plantea a los alumnos una investigación de carácter lúdico por la aparente falta de complejidad de
este tipo de números. El profesor ha de recalcar la idea de que los pitagóricos tenían una noción
intuitiva de número asociada a un punto, no tan abstracta como la que podemos tener en la actualidad.
Por otra parte se ha de resaltar el hecho de que eran fundamentalmente geómetras con un escaso
desarrollo de la aritmética al no contar con ningún sistema de numeración ágil y flexible, (de ahí su
necesidad de objetivar el concepto de número a través de puntos o como relación entre segmentos)

Actividad de investigación.

Material: Vídeo NÚMEROS TRIANGULARES Y NÚMEROS CUADRADOS.
PROGRAMA 19. Serie Ojo Matemático
 

Contenidos del vídeo

Hoja para el alumno.

Podemos representar los números enteros mediante colecciones de puntos. Cada punto representa una
unidad. Los siguientes números se pueden disponer formando un triángulo. Se les llama números
triangulares.

Observa en los cuatro primeros números triangulares cómo se forma cada triángulo a partir del anterior.

Para contar todos los puntos de un número triangular basta con que cuentes los puntos por columnas  empezando por la columna de la izquierda  y sumes los puntos de cada nueva columna.

a) Escribe los tres siguientes números triangulares:
______________________________________________

b) Rodea con círculo los números que sean triangulares:
     34   45   55   86   132

c) ¿Cuál es el décimo número triangular? ____________

d) ¿Y el décimo quinto? ___________

e) Escribe, sin dibujarlo,  el que ocupa el lugar 31 __________

f) Escribe una fórmula general para obtener cualquier número triangular :

g) ¿Cuántos choques de mano se producen cuando se encuentran 5 amigos? ___________________

h) ¿Y si son 6?__________

i) ¿Y si fueran 8?__________

Encuentra una fórmula general que nos proporcione el número de choques de mano cuando haya n personas. Encuentras alguna relación entre esta fórmula y los números triangulares.

En el vídeo el tendero intenta construir pirámides triangulares en las que cada piso esta formado por un número triangular de rollos de papel. Según subimos en la pirámide cada piso es el número triangular anterior hasta llegar a 1.

j) ¿Cuántos rollos se necesitan para construir una pirámide de 7 pisos? _____________________

k) ¿Se puede construir una pirámide triangular con 140 rollos? _________________________________

l) ¿Cuántos pisos tendría la pirámide triangular mas grande que podría construir sin pasarse de esos
140 rollos? ___________________________________

m) ¿Cuántos de los 140 le sobrarían? ______________________________________________

2. Números cuadrados

Los números cuadrados son aquellos cuyos puntos forman un cuadrado. Coinciden con los cuadrados
de los números enteros.
Comprueba que todo número cuadrado es suma de números impares consecutivos empezando por 1:
     1 = 1;    1 + 3 = 4 ;    1 + 3 + 5 = 9 ;     1 + 3 + 5 + 7 = 16

o) Escribe los 6 primeros términos de las secuencias de los números triangulares y cuadrados:
Nos Triangulares:   ___ , ___ , ___ , ___ , ___ , ___
Nos Cuadrados:      ___ , ___ , ___ , ___ , ___ , ___

Compara ambas secuencias. Escribe la relación que hay entre los números triangulares y los
cuadrados.

Las pirámides cuadradas se forman igual que las triangulares, pero ahora cada piso está formado por
un número cuadrado. Según asciendes cada piso es el número cuadrado anterior hasta llegar a 1.
Hay una relación entre las pirámides triangulares y las cuadradas. Para descubrirla haz estos cálculos:

p) ¿Cuántos rollos tiene una pirámide triangular de 5 pisos? _______________

q) ¿Cuántos rollos tiene una pirámide triangular de 4 pisos? _______________

r) ¿Cuántos rollos tiene una pirámide cuadrada de 5 pisos? _______________

s) Escribe la relación que hay entre las pirámides cuadradas y las triangulares:

3. Números pentagonales y hexagonales

t) Escribe las diez primeros números pentagonales. Intenta encontrar una fórmula para obtener
cualquier número pentagonal.

u) Haz lo mismo con los números hexagonales.

De hecho con estas actividades hemos podido abordar un alto porcentaje de contenidos del bloque de
Números del curriculum. Pero hay algo más: los materiales utilizados y la gradación de los niveles
de dificultad de las preguntas planteadas nos permite realizar en el aula un tratamiento preciso y claro
de la diversidad de los alumnos: no todos van a conseguir responder a todas las preguntas y sobre todo
no lo van a hacer siguiendo los mismos métodos ni con el mismo nivel de rigor y precisión.
Como el desarrollo de las actividades se produce en el menos tres sesiones, se pueden introducir
dinámicas de trabajo en pequeños grupos con intereses o niveles parejos o complementarios que
posibiliten al alumno un contraste de opiniones con sus compañeros y construir conocimientos a partir
de las ideas propias y ajenas.
Pero la ventaja de esta investigación, que no olvidemos ha surgido de una exploración histórica, es
que deja puertas abiertas para seguir profundizando en el estudio de regularidades numéricas más
complejas que nos pueden llevar de manera natural, (la actividad de los choques de manos ya nos lo
sugiere de manera clara), al estudio de técnicas de recuento relacionadas con el azar y la combinatoria.

De hecho si observamos el triángulo de Pascal, en la diagonal marcada aparecen los números triangulares, pero además en la inmediata inferior aparecen los números tetragonales, es decir, los que forman las pirámides triangulares, cuyos pisos son a su vez números triangulares.
Bastante más fácil es descubrir que en la diagonal superior aparecen los números naturales.
Como se puede observar sin mucho esfuerzo el triángulo de Pascal es algo mucho más rico en
relaciones numéricas que lo que tradicionalmente habíamos pensado al limitarlo a una mera tabla de
coeficientes del desarrollo del binomio de Newton.

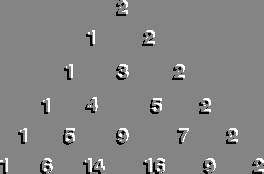Como sugerencia, y una vez que el profesor haya explicado cómo se obtienen los números del triángulo de Pascal (cada uno es la suma de los dos que tiene encima), podemos preguntar a esos alumnos que siempre nos demandan profundizar un poco más qué pasaría si cambiamos los unos de uno de los lados externos del triángulo de Pascal por doses.

¿Qué relaciones numéricas se pueden encontrar? ¿Qué sucedería si en lugar de doses colocamos treses o cuatros?

Como habéis podido comprobar, a partir de un pequeño hilo de la historia, en apariencia pueril e
intrascendente, hemos descubierto un ovillo sorprendente rico en relaciones numéricas que además
nos ha permitido asociar una serie de sucesiones numéricas, en un principio poco atractivas para los
alumnos, con una serie de modelos geométricos bastante más sugerentes que las meras fórmulas algebraicas de siempre.
La historia de las matemáticas es un mundo rico en situaciones similares. Es hora, siempre lo ha sido,
de aprovecharnos de ello y convertir a la Historia de las Matemáticas, en el poderoso recurso didáctico
que siempre ha debido ser.