http://math.etsu.edu/multicalc/prealpha/

Ejemplo 1.    Evaluar la siguiente integral doble

Ejemplo 2.    Evaluar

ó õ 2 0  ó õ x 1  x2ydydx

Solución: Primero se evalúa la integral interna:

ó õ 2 0  ó õ x 1  x2ydydx = ó õ 2 0  é ë ó õ x 1  x2ydy ù û dx = ó õ 2 0  é ë x2  y2 2 ê ê x 1  ù û dx = ó õ 2 0  é ë x2  x2 2 -x2  1 2 ù û dx = ó õ 2 0  é ë  x4 2 -  x2 2 ù û dx =  28 15

Ejemplo 3.    Evaluar

Ejemplo 4.    Evaluar

ó õ p 0  ó õ y 0  sin( y) dxdy

Solución: Considerando sin( y) constante:

ó õ p 0  ó õ y 0  sin( y) dxdy = ó õ p 0  é ë sin( y) ó õ y 0  dx ù û dy = ó õ p 0  [ ysin( y) ] dy

Integrando por partes con u = y  y  dv = sin( y) dy se tiene:

u = y dv = sin( y) dy du = dy v = -cos( y)         ó õ p 0  [ ysin( y) ] dy = -ycos( y) | 0p+ ó õ p 0  cos(y) dy

Luego,

ó õ p 0  ó õ y 0  sin( y) dxdy = -pcos( p) = p

Ejemplo 5.    Encontrar el volumen del sólido bajo el gráfico de  f( x,y) = 2-x²-y² sobre la región

x en [0,1] y = 0  a  y = x

LiveGraphics3d Applet
Mover con el mouse

Ejemplo 6.    Calcular el volumen del sólido bajo el gráfico de  f( x,y) = x²+y² sobre la región

Ejemplo 7.    Encontrar el volumen del sólido bajo el gráfico de f(x,y) = e^-x-y  sobre el primer cuadrante.

Mover con el mouse

Ejemplo 8.    Encontrar el volumen del sólido entre z = x+y  y   z = x-y sobre la región

V = R  ( ( x+y) -( x-y) )dA = R  2y dA

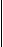
V = ó õ 1 0  2y x y y2 dy = ó õ 1 0  ( 2y·y-2y·y2) dy

Ejemplo 9.    Evaluar la integral iterada

ó õ 1 0  ó õ 1 x  sin( py2) dydx = R  sin( py2) dA

Como  Tipo I x = 0 y = x x = 1 y = 1                 Como Tipo II y = 0 x = 0 y = 1 x = y

Ejemplo 10.    Evaluar la integral iterada

ó õ 1 -1  ó õ 1 | y|   sinh( y3) cos( x2)   dxdy

Solución: La  integral iterada no se puede calcular en la forma propuesta, por ello se expresa como integral doble:

ó õ 1 0  ó õ 1 | y|   sinh( y3) cos(x2)   dxdy = R  sinh( y3) cos(x2)   dA

La región de integración R se puede presentar como:

Como Tipo II y = -1 x = | y| y = 1 x = 1                 Como Tipo I x = 0 y = -x x = 1 y = x

Consecuentemente:

R  sinh( y3) cos( x2)   dA = ó õ 1 0  ó õ x -x  sinh( y3) cos(x2) dydx = ó õ 1 0  cos( x2) é ë ó õ x -x  sinh(y3) dy ù û dx

La integral ineterior no se puede calcular, pero como sinh( y³)  es impar, se tiene

ó õ x -x  sinh( y3) dy = 0

Así la integral completa debe ser igual a 0, es decir

ó õ 1 -1  ó õ 1 | y|   sinh( y3) cos( x2)   dxdy = 0

Ejemplo 11.    Encontrar y describir la imagen de [ 0,2p] ×[ 0,1] bajo la transformación

Solución: Como x = 2vcos( u)  e  y = vsin(u), se tiene

x2 4 +  y2 1 = v2cos2( u) +v2sin2( u) = v2

como u varía de 0 a 2p es una elipse centrada en el origen. Además, estas elipses cubren completamente la región interior de la elipse correspondiente a  v = 1. EL Jacobiano de la transformación es

¶( x,y) ¶( u,v) = æ è  ¶ ¶u 2vcos( u) ö ø æ è  ¶ ¶v vsin( u) ö ø - æ è  ¶ ¶v 2vcos( u) ö ø æ è  ¶ ¶u vsin( u) ö ø = -2vsin2( u) -2vcos2( u) = -2v

Así, dA = 2vdvdu y el área de la región imagen es

Area  of  R = ó õ ó õ S  ê ê  ¶( x,y) ¶( u,v) ê ê dvdu = ó õ 2p 0  ó õ 1 0  2vdvdu = ó õ 2p 0  v2  1 0 du = ó õ 2p 0  du = 2p

Ejemplo 12.    Evaluar òò_R( x+y) dA donde  R  es la región con fronteras  y = x,  y = 3x,  y  x+y = 4

Solución: T( u,v) = áu-v,u+v ñ  es equivalente a  x = u-v, y = u+v. Luego:

y = x    Þ     u+v = u-v    Þ    2v = 0    Þ     v = 0 y = 3x    Þ     u+v = 3u-3v    Þ    4v = 2u    Þ     v =  u 2 x+y = 4    Þ     u-v+u+v = 4    Þ    2u = 4    Þ     u = 2

Esto es, S es la región acotada por  v = 0, v = u/2, u = 2. El Jacobiano de la transformación es

¶( x,y) ¶( y,v) =  ¶x ¶u  ¶y ¶v -  ¶x ¶v  ¶y ¶u = 1·1-( -1) ·1 = 2

Así, dA = 2dvdu, luego

òòR ( x+y) dA =   òòS  ( u-v+u+v) 2dvdu = ó õ 2 0  ó õ u/2 0  4udvdu = 16/3

ó õ 2 1  ó õ x+3 x+2   dy dx xy-x2

ó õ 2 1  ó õ x+3 x+2   dy dx xy-x2  =  ó õ ó õ R   1 xy-x2   dA

Para calcular el Jacobiano observar que x = u, y = u+v implica

ó õ ó õ R   1 xy-x2 dA = ó õ 2 1  ó õ 3 2   1 u( u+v) -u2   du dv = ó õ 2 1  ó õ 3 2   1 u2+uv-u2   du dv = ó õ 2 1  ó õ 3 2   1 Ö uv  du dv

ó õ 2 1  ó õ x+3 x+2   dy dx xy-x2 = ó õ 2 1  ó õ 3 2  u-1/2v-1/2dudv = 4Ö2Ö3-8-4Ö3+4Ö2

Ejemplo 14.    Usar T( u,v) = áu²,v ñ para evaluar

ó õ 1 0  ó õ Öx 0  yeÖx dydx

Solución: La región  de integración R es acotada por las curvas  x = 0,  x = 1, y = 0, e  y = Öx. Ya que x = u² e  y = v, se tiene

x = 0    Þ     u = 0 x = 1    Þ     u = 1 y = 0    Þ     v = 0 y = Öx    Þ     v = u

Además, como x = u²  e  y = v se tiene que

¶( x,y) ¶( u,v) = æ è  ¶ ¶u u2 ö ø æ è  ¶  ¶v v ö ø - æ è  ¶  ¶v u2 ö ø æ è  ¶ ¶u v ö ø = 2u

Así, dA = 2ududv, se tiene

ó õ 1 0  ó õ Öx 0  yeÖx dydx = ó õ ó õ R  yeÖx  dA = ó õ 1 0  ó õ u 0  veu  2u  dvdu = ó õ 1 0  u3eudu = -2e+6

Solución: Expresando la integral iterada como una integral doble, se tiene

ó õ Ö3 0  ó õ Ö y2+9 2y   sin(x2-y2) x2-y2 dxdy = ó õ ó õ R   sin(x2-y2) x2-y2 dA

donde R es la región acotada por  y = 0,  x = 2y, y  x² = y²+9.La transformación inversa que trae R  a S  se obtiene colocando  x = vcosh(u) and y = vsinh( u) :

y = 0    Þ     vsinh( u) = 0   Þ     v = 0  or  sinh( u) = 0    Þv = 0  or  u = 0 x = 2y    Þ     vcosh( u) = 2vsinh(u)     Þ     tanh( u) = 0.5   Þ     u = tanh-1( 0.5) x2 = y2+9    Þ     v2cosh2( u)-v2sinh2( u) = 9    Þ     v2 = 9

Así S es u = 0, u = tanh^-1( 2) , v = 0, v = 3.

A continuación calculamos el Jacobiano:

¶( x,y) ¶( u,v) =  ¶x ¶u  ¶y ¶v -  ¶x ¶v  ¶y ¶u = vsinh( u) sinh( u) -cosh( u)vcosh( u) = -v( cosh2( u) -sinh2( u) ) = -v

Así, dA = | -v| dudv = vdudv ya que v está al interior de S. Como x²-y² = v², la integral doble queda

ó õ ó õ R   sin( x2-y2) x2-y2 dA = ó õ 3 0  ó õ tanh-1( 0.5) 0   sin(v2) v2 vdudv = ó õ 3 0      sin( v2) v u ê ê tanh-1( 0.5) 0    dv = tanh-1( 0.5) ó õ 3 0   sin( v2) v dv

Finalmente, la integral que aparece puede ser estimada numéricamente.

ó õ Ö3 0  ó õ Ö y2+9 2y   sin(x2-y2) x2-y2 dydx = tanh-1( 0.5) ó õ 3 0   sin( v2) v dv » 0.4573

Ejemplo 16.    Usar coordenadas polares para evaluar

ó õ 1 0  ó õ Ö 2-x2 ( x2+y2)dydx =   ( x2+y2) dA x

Como r² = x²+y², la integral doble queda

( x2+y2) dA = ó õ p/2 p/4  ó õ Ö2 0  r2  rdrdq = ó õ p/2 p/4  ó õ Ö2 0  r3  drdq

y la resultante integral iterada resultante, puede ser fácilmente calculada:

( x2+y2) dA = ó õ p/2 p/4   r4 4 ê ê Ö2 0  dq = ó õ p/2 p/4  dq =  p 4

Un importante resultado en estadística

El cálculo de la integral

I = ó õ ¥ 0  e-x2dx

es importante en aplicaciones estadísticas. Para evaluarla, en primer lugar observar que

I 2 = é ë ó õ ¥ 0  e-x2dx ù û é ë ó õ ¥ 0  e-y2dy ù û = ó õ ¥ 0  ó õ ¥ 0  e-x2e-y2dydx

Es decir, I ² es una integral iterada que puede ser transformada usando coordenadas polares.       
 

Ejemplo 17.    Evaluar la integral

ó õ ¥ 0  e-x2dx = p 2           y          ó õ ¥ -¥  e-x2dx =   p

Ejemplo 18.    Determinar el volumen del sólido entre x = yz  y  x = 0 sobre la región y = 0, y = 1, z = 0, z = 4.

Solución: El volumen viene dado por

V =  dV = ó õ yz 0  dx  dA1

Sustituyendo las fronteras de R se tiene la integral triple iterada

V = ó õ 4 0  ó õ 1 0  ó õ yz 0  dxdydz

Luego

V = ó õ 4 0  ó õ 1 0  yz  dydz = ó õ 4 0  z  y2 2 ê ê y = 1 y = 0  dz = ó õ 4 0   z 2 dz = 4