|
U1: Geometría
analítica Sesión: La hipérbola |
|
|
|
|
|
|
|
| 1) | La hipérbola (Documento para la clase) |
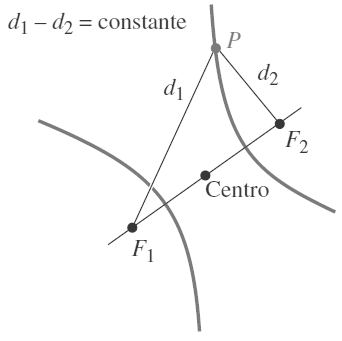
| a) ¿Qué es la hipérbola? | |
| - Mirada geométrica con GeoGebra. Directriz y Focos | |
| - Mirada algebraica: La ecuación de la hipérbola | |
| b) Elementos asociados a una hipérbola | |
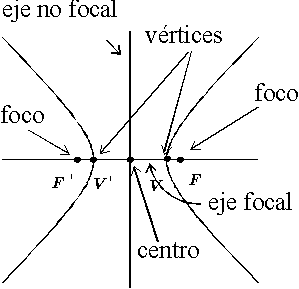 |
|
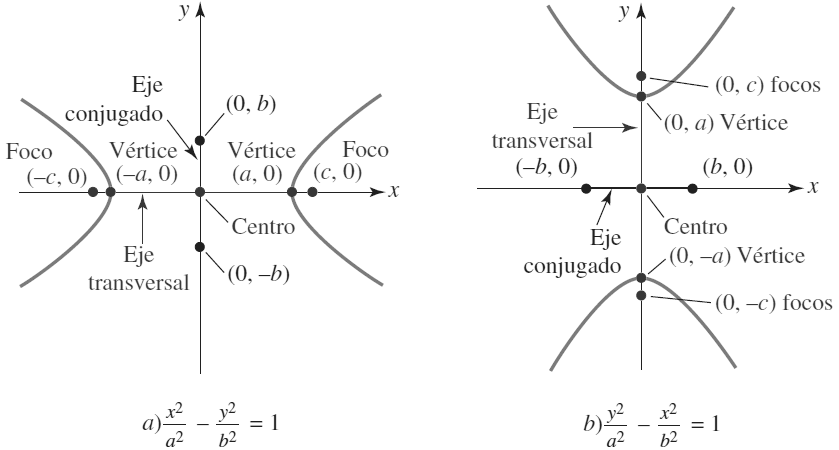
| 2) | Resumen ecuaciones de la hipérbola con vértive en el origen |
|
|
|
| 3) | Actividad: Determinar la ubicación de vértices y focos de la hipérbola $9x^2 - 25y^2 = 225$. Trazar la gráfica |
| 4) | Hipérbola con centro $(h,k)$ y eje paralelo a un eje coordenado |
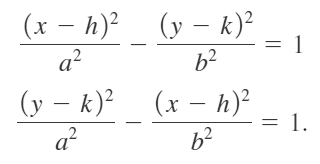 |
|
| 5) | Actividad: Verificar que la ecuación $4x^2 -y^2 - 8x - 4y - 4 = 0$ representa una hipérbola. Indicar su centro, vértices y focos. Obtener su gráfico. |
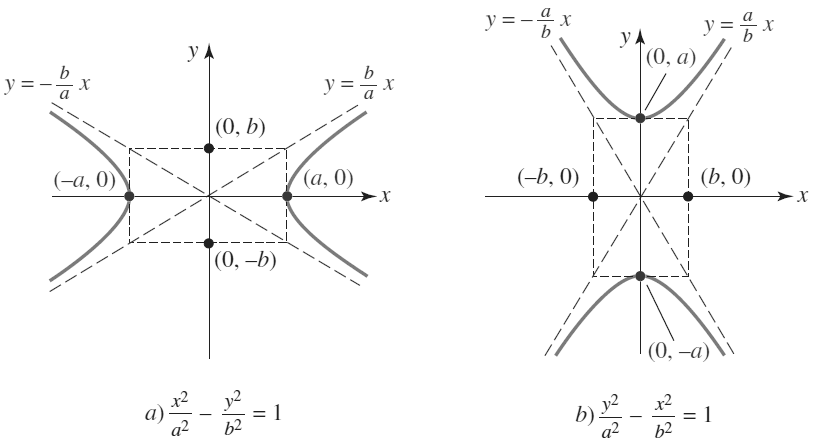
| 6) | Asíntotas a la hipérbola |
|
|
|
| 7) | Actividad: Determinar la ecuación de la hipérbola cuyos vértices están en $(0, -4)$ $(0, 4)$ y sus asíntotas son $y =-\frac{1}{2}x$ e $y=\frac{1}{2}x$ |
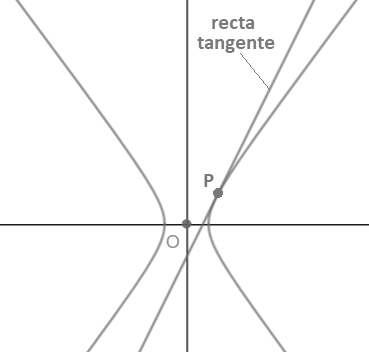
| 8) | Hipérbolas y rectas tangentes |
|
|
|
| 9) | Actividad: Hallar las ecuaciones de la rectas tangente y normal a la hipérbola $ \frac{x^2}{36}-\frac{y^2}{64}=1$ en su punto de abcisa $x=8$ y considerando que el punto se encuentra en el primer cuadrante. |
| 10) | Aplicaciones de la hipérbola |
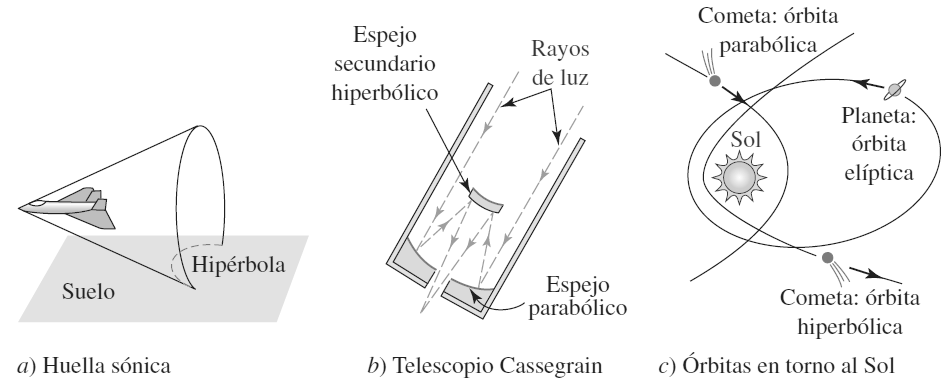 |
|
|
Bibliografía básica:
|
|
|
|
|
|
U1: Geometría
analítica Sesión: La parábola |
|