Resolución de problemas en la enseñanza de la matemática
 |
Resolver
problemas es un arte práctico, igual que nadar o jugar fútbol: se puede
aprender sólo por imitación y práctica... si alguien desea aprender a nadar
debe ir al agua, y si alguien desea ser un buen resolvedor de problemas debe
resolver problemas. George
Polya (1961) |
·
¿Qué es un problema?

A continuación se presentan algunas explicaciones, que diferentes
autores han entregado, sobre qué es un problema.
|
-
Tener un problema significa buscar, de forma consciente, una acción
apropiada para lograr un objetivo claramente concebido, pero no alcanzable de
manera inmediata. Mathematical Discovery, G. Polya, 1961
-
Para que una situación constituya un problema para una persona, ésta
debe estar enterada de la existencia de la situación, reconocer que debe
ejecutar algún tipo de acción ante ella, desear o necesitar actuar, hacerlo y
no estar capacitado, al menos en lo inmediato, para superar la situación, Teaching and Learning Mathematics, F. Bell, 1978
-
Un problema es una situación cuantitativa o de otra clase, a la que se
enfrenta un individuo o un grupo, que requiere solución, y para la cual no se
vislumbra un medio o camino aparente y obvio que conduzca a la misma. Problem Solving, a handbook for teachers, S. Krulik y K. Stacey, 1980
-
Una situación constituye un problema para una persona, cuando dicha
situación no es familiar para ella, es decir, cuando la novedad es la
característica fundamental de la misma y cuando requiere un tratamiento
distinto de una simple aplicación rutinaria. Dicho en términos de ejecución,
cuando su resolución necesita de una deliberación, identificación de posibles
hipótesis y comprobación de factibilidad, teniendo el individuo que elaborar
conductas propias que pongan a prueba sus capacidades de razonamiento autónomo. La resolución de problemas: ¿una panacea metodológica?, L. Contreras,
1987
-
Un problema constituye primeramente una situación objetiva que se
presenta y evidencia como dificultades cognitivas, carencias de información,
contradicciones ideativas, o necesidades diversas, no solucionables espontánea
y trivialmente, sino superables sólo mediante un reflexivo estudio o
investigación teórica, empírica o aplicada, que se efectúe oportunamente. Problema, Problemática, Problematización; A. Becerra, 1989
-
Tengo un verdadero problema cuando me encuentro en una situación desde
la que quiero llegar a otra, unas veces bien conocida otras un tanto
confusamente perfilada, y no conozco el camino que me puede llevar de una a
otra. Tendencias innovadoras en educación matemática, M. de Guzmán, 1993
·
Diferencias entre problema y ejercicio
· Aspectos que influyen en la capacidad de resolver problemas:
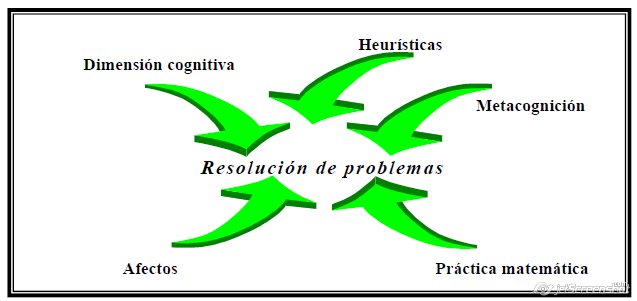
Desde el punto de
vista de los diferentes aspectos que influyen en la resolución de problemas,
Alan Schoenfeld propone cinco dimensiones que intervienen directa, dinámica e
interrelacionadamente:
-
Dimensión cognitiva: La base de
conocimientos.
-
Heurísticas: Estrategias en la
resolución de problemas.
-
Dimensión
metacognitiva: Monitoreo y control (auto-regulación).
-
Dimensión afectiva: Creencias y
afectos.
-
Práctica matemática: Experiencia en la
resolución de problemas.
Los conocimientos
que el resolvedor tenga en el
ambiente matemático donde se ha planteado el problema (resultados,
definiciones, procedimientos algorítmicos, procedimientos rutinarios, fórmulas,
reglas, etc.) tienen una incidencia directa en la factibilidad de acceder a una
solución del problema. Por su parte, con
respecto a las estrategias en la resolución de problemas (heurísticas), que el resolvedor tenga incorporadas
naturalmente, tales como: analogía, elementos auxiliares, descomponer y recombinar,
inducción, particularización, generalización, variación, trabajando hacia
atrás, etc.; diversas investigaciones han demostrado que también juegan un rol
fundamental a la hora de intentar resolver un problema. La auto-regulación
en el trabajo (monitoreo y control), es decir la capacidad del resolvedor para decidir qué, cuándo y
cómo usar una determinada estrategia o resultado matemático; cuando abandonar
(al menos temporalmente) un camino de solución, son capacidades metacognitivas
que influyen fuertemente en la resolución de problemas. Con respecto a la
dimensión afectiva, las creencias que el
resolvedor tenga acerca de la naturaleza de la matemática, por ejemplo: los problemas matemáticos tienen solamente
una solución correcta; hay solamente
una manera correcta de resolver un problema; si uno entiende el contexto matemático, todo problema puede ser
resuelto en diez minutos o menos, etc. enmarcarán el quehacer del
estudiante durante el proceso de resolver un problema[1].
Por su parte, el grado en que el resolvedor disfruta el proceso de resolución
de problemas y su capacidad para superar la frustración del fracaso en obtener
la solución de algunos problemas, son aspectos afectivos que inciden en la
actitud del resolvedor. Finalmente, la
práctica matemática a que ha sido expuesto un estudiante en la escuela, es un
factor que afectará su capacidad para resolver problemas. Diversos estudios y
experiencias muestran que cuando el profesor diseña ambientes donde se
privilegia la interacción de los estudiantes y se promueve el pensamiento
matemático, el alumno adquiere una actitud favorable hacia la actividad de
resolver problemas.
·
Propuestas metodológicas para
resolver problemas
( . .
. no hay camino, se hace camino al andar. )
G. Polya Con respecto a los métodos para resolver
problemas, fue el matemático húngaro, George Polya quien en su libro publicado
en el año 1945, How to solve it, sentó las bases modernas de esta línea de
reflexión e investigación. Resumidamente, la propuesta de Polya[2],
contempla cuatro fases en la resolución de problemas. En cada una de ellas,
Polya plantea interrogantes claves con el objetivo de guiar y orientar la
acción de la persona que intenta resolver un problema:
1)
Comprender el problema.
-
¿Cuál es la incógnita?.
-
¿Cuáles son los datos?.
2)
Concebir un plan.
-
¿Se ha encontrado con un problema semejante?
-
¿Conoce un problema relacionado con éste?
-
¿Podría enunciar el problema de otra manera?
-
¿Ha empleado todos los datos?
3)
Ejecutar el plan.
-
¿Son correctos todos los pasos dados?
4)
Examinar la solución obtenida (Mirando hacia atrás).
-
¿Puede verificar el resultado?
-
¿Puede verificar los razonamientos realizados? A continuación se presenta un listado de las estrategias que
normalmente usamos los profesores de matemática (junto a nuestros estudiantes)
cuando intentamos resolver un problema. Como es de suponer, este listado no
pretende ser exhaustivo (es imposible que lo sea) ni disjunto.
1.
Hacer uso de una o más fórmulas.
2.
Hacer uso de uno o más teoremas.
3.
Empezar por lo
fácil: simplificar o buscar casos particulares (dividir para conquistar). Elegir valores especiales para
ejemplificar el problema y, a partir de ellos, intentar obtener alguna sugerencia para la solución. Incorporar
argumentos del tipo sin pérdida de generalidad,
por ejemplo asignar a uno de los datos un valor cómodo.
4.
Experimentar y
buscar regularidades (patrones).
5.
Modificar el problema: reformularlo y buscar metas
parciales.
6.
Prueba y error.
7.
Organizar la
información: Siempre que sea posible, hacer un esquema, una tabla, una figura,
un diagrama.
8.
Escoger un lenguaje adecuado, una notación
apropiada.
9.
Analizar posibles simetrías y casos extremos (los
casos límites, en general, permiten explorar el rango de posibilidades).
10.
Suponer el problema resuelto (trabajar hacia atrás).
11.
Proponer un problema
semejante, lo más sencillo posible y tratar de resolverlo; luego, proceder a
complicarlo hasta llegar al propuesto inicialmente.
12.
Observar la
incógnita y pensar en un problema que le sea familiar y que tenga la misma (o
similar) incógnita.
13.
Considerar problemas
equivalentes:
a)
Reemplazar las condiciones por otras equivalentes.
b)
recombinar los elementos del problema de diferentes
maneras.
c)
Introducir elementos auxiliares.
d)
Reformular el problema:
i)
Cambiar la perspectiva o notación.
ii)
Intentar argumentos
por contradicción (¿qué pasaría si lo que queremos verificar no se cumple?) o
contrapositiva (si queremos comprobar que A
Þ B, tratar de verificar que
~B
Þ
~A).
iii)
Suponiendo que se tiene la solución, determinar sus
propiedades. Bibliografía.
[1] Como es de suponer, también en este aspecto influyen las creencias del profesor y las sociales, sobre la resolución de problemas [2] Las ideas de Polya, tienen su antecedente más directo en el trabajo de R. Descartes: Rules for the Direction of the Mind.
|