Palamedes |
Personaje mitológico, a quien la tradición griega atribuye el invento de los números. Platón ironizaba: «¿De manera que Agamenón, antes de Palamedes, no sabía cuántos pies tenía?» (República 522e).  |
Palamedes |
Personaje mitológico, a quien la tradición griega atribuye el invento de los números. Platón ironizaba: «¿De manera que Agamenón, antes de Palamedes, no sabía cuántos pies tenía?» (República 522e). |
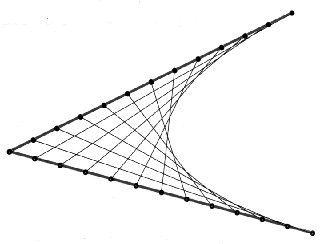  Hay muchas formas de trazar una parábola. El método del sastre es uno de los más sencillos. Lo usan esos profesionales cuando quieren coser una tela en forma de curva.Se
dibuja un ángulo cualquiera. Se marcan divisiones iguales en cada uno de los dos lados, numeradas empezando en ambos casos por el vértice. Se unen los puntos cuyos valores suma una constante, por ejemplo 11, (se puede hacer con cualquier otro número). La envolvente de las rectas obtenidas es una parábola. La
ciudad norteamericana de San Luis, a orillas del Mississippi, da la bienvenida a sus visitantes con un enorme arco en forma de parábola. Es el Gateway Arch, que mide 192 metros de altura. Este impresionante monumento simboliza el papel de San Luis como "puerta de entrada" al Oeste americano. |
 El padre del pequeño Blas Pascal no queria que su hijo estudiase matemáticas. Prefería que dedicase sus esfuerzos a las lenguas antiguas. Pero aquel chico era un prodigio con los números. Según el relato (seguramente exagerado) de su hermana, Blas descubrió en su adolescencia por sí solo numerosos teoremas de Euclides. En vista de semejante prodigio, su padre no tuvo más remedio que ceder y dejarle estudiar matemáticas. A los catorce años fue admitido en una prestigiosa academia. A los dieciséis publicó su primer libro sobre geometría. A los diecinueve consiguió construir una máquina calculadora que ayudaba a su padre -recaudador de impuestos- en sus pesados cálculos. Era la tatarabuela de las calculadoras actuales.Su
correspondencia con el matemático Fermat sobre el juego de los dados dio origen a la teoría del cálculo de probabilidades. A
él se debe el triángulo aritmético o triángulo de Pascal, asi como numerosos descubrimientos en Física. Siendo
ya muy mayor, se hizo miembro de una secta, la jansenista, y pasó el resto de su vida dedicado a la meditación y a la redacción de obras religiosas. |
 Karl Pearson (1857-1936) nace en Londres y estudia Derecho en Cambridge, siguiendo la tradición familiar, aunque él siempre había destacado en matemáticas. Posteriormente simultanea actividades políticas y literarias y a los veintisiete años comienza a impartir clases de matemáticas en la universidad de Londres. Muy pronto se sintió interesado por la aplicación de las matemáticas al estudio de la evolución de las especies y la herencia. En 1901 funda la revista Biometrika, en la que publica una monumental biografía sobre Galton. A Pearson se deben aportaciones tan importantes en estadística como el coeficiente de correlación lineal, la distribución  o el test de Pearson para el estudio de la bondad del ajuste de una distribución empírica mediante una teórica. A Galton y a Pearson se les considera hoy día los padres de la Estadística moderna. |
Le rodean muchos misterios, a pesar de ser una constante natural. Aparece en los lugares más inesperados: la probabilidad de que dos enteros positivos cualesquiera sean primos entre sí es 6/  2. Augustus de Morgan escribió "... este misterioso 3.14159... que se cuela por todas las puertas y ventanas, que se desliza por cualquier chimenea". Bertrand Russell escribió un cuento corto titulado La pesadilla del matemático, en el que escribe "El rostro de estaba enmascarado; se sobreentendía que nadie podía contemplarlo y continuar con vida. Pero unos ojos de penetrante mirada acechaban tras la máscara, inexorables, fríos y enigmáticos...".Las
primeras civilizaciones indoeuropeas ya tenían conciencia de que el área del círculo es proporcional al cuadrado de su radio, y de que su circunferencia lo es al diámetro. Sin embargo no se sabe cuándo se comprendió por vez primera que ambas razones son la misma constante, simbolizada en nuestros días por la letra griega (El símbolo del que toma nombre la constante lo introdujo en 1706 el escritor y matemático inglés William Jones y lo popularizó el matemático suizo Leonhard Euler (v.) en el siglo XVIII.) Arquímedes de Siracusa (v.), el mayor matemático de la antigüedad, estableció rigurosamente la equivalencia de ambas razones en su tratado Medición de un circulo. Usando polígonos de 96 lados inscritos (idea de Antífono) y circunscritos (idea de Brisón de Heraclea) (¡y sin conocer las funciones trigonométricas!), llegó a que 310/71<<310/70 y dedujo un laborioso procedimiento para calcular con cualquier precisión. En el s. V, el astrónomo chino Tsu Ch'ung-Chih descubrió que  . Todos los intentos de calcular el número realizados en Europa hasta mediados del siglo XVII se fundaron de un modo u otro en el método de Arquímedes. Ludolph van Ceulen, matemático holandés del siglo XVI, dedicó gran parte de su carrera al cálculo de . Casi al final de su vida obtuvo una aproximación de 32 cifras calculando el perímetro de polígonos inscritos y circunscritos de 262 (unos 1018) lados. Se dice que el valor de que obtuvo así, denominado número ludolfiano en ciertas regiones de Europa, fue su epitafio.Los
que investigando la cuadratura del círculo creyeron haber descubierto un valor exacto de forman legión; ninguno de ellos aventajó al filósofo inglés Thomas Hobbes en capacidad para combinar con un elevado pensamiento la más profunda ignorancia. En la época de Hobbes no se les enseñaban las matemáticas a los ingleses cultivados, y éste había ya cumplido los cuarenta cuando por vez primera ojeó los textos de Euclides. Al llegar al teorema de Pitágoras exclamó asombrado: «¡Por Dios! ¡Esto es imposible!», tras de lo cual retrocedió y rehizo paso a paso toda la demostración hasta quedar plenamente convencido. Durante el resto de su vida se entregó a la geometría con el ardor de un enamorado. «La geometría tiene algo que la asemeja al vino», escribiría posteriormente, y se dice que, a falta de superficies más adecuadas, solía dibujar figuras geométricas en la ropa de su cama. Si Hobbes se hubiera contentado con ser un matemático aficionado, un amateur, hubieran sido más tranquilos los años de su vejez; pero su monstruoso egotismo le indujo a creerse dotado para realizar grandes descubrimientos en matemáticas. En 1655, a los sesenta y siete años de edad, se lanzó a publicar un libro en latín titulado De corpore (Sobre los cuerpos), en el que figuraba un ingenioso método para cuadrar el círculo. En realidad, el método no era más que una excelente aproximación, pero Hobbes estaba convencido de su exactitud. John Wallis, un distinguido matemático y criptógrafo inglés escribió entonces un folleto poniendo en evidencia los errores de Hobbes, y de este modo comenzó uno de los más largos, divertidos y estériles duelos verbales que jamás hayan librado dos espíritus selectos. Durante casi un cuarto de siglo, ambos contendientes se dirigieron los más hábiles sarcasmos y las más aceradas invectivas. Wallis mantuvo la disputa, en parte por propia diversión, pero principalmente porque veía en ella un modo de ridiculizar a Hobbes, creando al mismo tiempo la duda acerca de sus opiniones políticas y religiosas, que Wallis detestaba. Hobbes respondió al primer ataque de Wallis haciendo reimprimir su libro en inglés e incluyendo un ultílogo titulado Six Lessons to the Professors of Mathematics... (Seis lecciones para profesores de matemáticas...) (Confío en que el lector sabrá disculpar que abrevie los interminables títulos de las obras del siglo XVII.) Wallis replicó con Due Correction for Mr. Hobbes in School Discipline for not saying his Lessons right (Castigo escolar impuesto al señor Hobbes por no dar debidamente sus lecciones). Hobbes contraatacó entonces con Marks of the Absurd Geometry, Rural Language, Scottish Church Politics, and Barbarisms of John Wallis (Notas sobre la geometría absurda, el lenguaje patán, la política de la Iglesia escocesa y otros barbarismos de John Wallis). Wallis devolvió el fuego con Hobbiani Puncto Dispunctio! or the Undoing of Mr. Hobbes' Points (Hobbiani Puncto Dispunctio! o La refutación de los puntos del Sr. Hobbes). Algunos panfletos más tarde (mientras tanto, Hobbes había publicado anónimamente en París un absurdo método de duplicación del cubo), Hobbes escribía: «O bien sólo yo estoy loco, o ellos (los profesores de matemáticas) han perdido por completo el juicio: no podemos, pues, aceptar una tercera opinión, a menos que aceptemos que todos estamos locos.» «La refutación está de más —fue la respuesta de Wallis—. Pues si él está loco, seguramente no atenderá a razones; por otra parte, si somos nosotros los locos, tampoco nos encontraremos en condiciones de intentar convencerle.» Con treguas momentáneas, la batalla prosiguió hasta la muerte de Hobbes, ocurrida a los noventa y un años. En uno de sus últimos ataques contra Wallis, Hobbes, que era efectivamente muy tímido en su relación con los demás, escribió: «El Sr. Hobbes jamás ha intentado provocar a nadie; pero quien le provoque descubrirá que su pluma es al menos tan hiriente como la suya. Todos vuestros escritos no son sino errores o sarcasmos; esto es, nauseabundos flatos, hedores de mulo viejo cinchado en exceso tras un hartazgo. Yo he cumplido. Os he tenido en consideración por esta vez, pero no lo repetiré...» . No es éste el lugar indicado para explicar con detalle lo que Wallis denominaba «la curiosa incapacidad del señor Hobbes para aprender lo que no sabe». En conjunto, Hobbes publicó alrededor de una docena de métodos diferentes para cuadrar el círculo. Una de las mayores dificultades que debió afrontar el filósofo fue su incapacidad para concebir que, considerados en abstracto, los puntos, las líneas y las superficies pudieran tener menos de tres dimensiones. En Quarrels of Authors (Autores en disputa), Isaac Disraeli escribe: «A pesar de todos los razonamientos de todos los geómetras que le rodeaban, parece ser que descendió a su tumba con la firme convicción de que las superficies tenían tanto extensión como profundidad.» Hobbes constituye un caso clásico de hombre de genio que se aventura en exceso por una rama de la Ciencia sin poseer la preparación necesaria, y que disipa sus prodigiosas facultades en vacuidades pseudocientíficas.Parientes
próximos de quienes se esforzaron en realizar la cuadratura del círculo fueron los computadores de , hombres que dedicaron años a la tarea de ir determinando cada vez más cifras decimales del número . Evidentemente, el único procedimiento para ello es emplear algún algoritmo infinito que converja hacia . El propio Wallis descubrió en 1665 uno de los más sencillos:  . El desarrollo del cálculo diferencial, obra en gran parte de Isaac Newton (v.) y Gottfried Wilhelm Leibniz (v.), permitió calcular de forma mucho más expedita. El propio Newton calculó con 15 decimales sumando unos cuantos términos de una serie, y posteriormente confesó "Me da vergüenza confesar a cuántas cifras llevé esos cálculos, que realicé por no tener otra cosa que hacer en aquel momento". En 1674 Leibnitz dedujo su fórmula  , de convergencia exasperantemente lenta, sobre un desarrollo del arco tangente descubierto por el escocés James Gregory. En 1706, John Machin descubrió su fórmula  , donde  , con la que pudo calcular los 100 primeros decimales de . En 1844, Johann Dase, calculador mental prodigioso capaz de multiplicar de memoria dos números de 100 cifras en 8 horas, calculó en cosa de unos meses 205 cifras de basándose en una variante de la fórmula de Machin.El
más constante entre todos los que se dedicaron al computo de fue el matemático inglés William Shanks. Trabajando durante veinte años obtuvo 707 decimales en 1853. Desdichadamente, el pobre Shanks cometió un error en el 528° decimal, y a partir de él todos los restantes están mal. (El error no fue descubierto hasta 1945, 92 años después, y los 707 decimales de Shanks figuran todavía en muchos textos.) En 1949 John Von Neumann utilizó la computadora electrónica ENIAC durante setenta horas de máquina con el objeto de calcular las primeras 2037 cifras decimales de ; posteriormente otra computadora invirtió tan sólo trece minutos en las primeras 3.000. Para 1959, una computadora emplazada en Inglaterra y otra en Francia habían rebasado la cota de las primeras 10.000. El millón de cifras fue logrado por Jean Guilloud y M. Bouyer en un día con una CDC 7600. En 1986 David H. Bailey extrajo 29.360.000 cifras en un Cray-2 de la NASA con un algoritmo de Ramanujan (v.) de convergencia cuártica (cuadruplicación del número de cifras en cada iteración). En 1987, centenario del nacimiento de Ramanujan (v.), Kanada consiguió más de 100 millones de cifras, y se podrían conseguir fácilmente 2.000 millones de cifras usando en exclusiva un superordenador durante una semana. En su libro The Lore of Large Numbers, Philip J. Davis escribe "El misterioso y maravilloso número se ha visto reducido a un gargarismo con el que las máquinas de calcular se aclaran la garganta".El
caso es que con 39 cifras basta para calcular la longitud de una circunferencia que abarque todo el universo con un error menor que el radio de un átomo de hidrógeno. ¿Porqué entonces calcular tantas cifras? Pues porque es una prueba de la potencia de las computadoras, porque abre inesperados campos en teoría de números, y... simplemente porque el problema "está ahí". No se ha probado que sus cifras sigan una distribución aleatoria; cabe en lo posible que a partir de un lugar deje de aparecer, por ejemplo, el 5. Hasta el momento, todos los ensayos estadísticos efectuados sobre la sucesión de cifras decimales de
han confirmado su carácter aleatorio. Esto quizá resulte un poco desconcertante para quienes piensen que debiera existir una relación un poco menos irregular entre la longitud y el diámetro de una curva tan simple y bella como la circunferencia, pero la mayor parte de los matemáticos se inclinan a creer que nunca se encontrará el menor orden ni regularidad en el desarrollo decimal de . Si es cierto que las cifras de forman una sucesión aleatoria, quizá esté justificado que presentemos aquí una curiosa paradoja, parecida al conocido aserto de que si una banda de monos aporreara durante suficiente tiempo unas cuantas máquinas de escribir, llegarían a dactilografiar las obras completas de Shakespeare. Stephen Barr ha señalado que si se pudieran materializar y medir con una precisión ilimitada dos barras, entonces estas dos barras, sin ninguna otra señal ni grabado sobre ellas podrían contener toda la Encyclopaedia Britannica. Una de las barras se tomaría como unidad; la otra habría de diferir de esta unidad en una fracción cuya expresión decimal será un número muy largo. Este decimal permitiría poner en clave toda la Britannica por el sencillo procedimiento de asociar con cada palabra y cada signo ortográfico del idioma un número diferente que no contenga ningún cero, pues éstos se utilizarán para separar las palabras y los signos del texto cifrado. Evidentemente, de este modo se puede encerrar toda la Enciclopaedia en un solo número, aunque de longitud casi inconcebible. Si ahora se coloca una coma al principio de este número y un 1 delante de la coma, se obtiene la longitud de la otra barra de Barr. ¿Y dónde interviene ? Bueno, si las cifras de son efectivamente aleatorias, en algún lugar del pastel infinito de sus cifras habrá una ración que contenga a la Britannica; y para abundar en el mismo tema, lo mismo ocurrirá con cualquier otro libro que se haya escrito, que se vaya a escribir o que en el futuro se pueda escribir.
|
Pitágoras de Samos |
Fundó en Crotona, Magna Grecia, la primera escuela-internado del mundo. Sus alumnos recitaban los Versos Aúreos al amanecer, al compás de la lira. Epitafio esculpido en piedra por su profesor Ferécides de Siros: "Pitágoras fue el primero de los griegos." Los
sabios de la antigüedad griega utilizaron sus conocimientos sobre circunferencias y esferas para crear un modelo matemático que describiera los movimientos de las estrellas y de los planetas. Pitágoras suponía que las estrellas estaban. fijadas a una esfera de cristal que daba diariamente una vuelta sobre si misma en torno a un eje que pasaba a través de la Tierra y que los siete planetas -Sol, Luna, Mercurio, Marte, Júpiter, Venus y Saturno- estaban cada uno anclado a su propia esfera móvil. Esta idea, que se convertiría en la teoría del movimiento de los cuerpos celestes, fue el fundamento de la astronomía hasta el siglo XVI. Pitágoras
nació en la isla de Samos y conoció a Thales, quién le animó a desplazarse hasta Egipto para estudiar matemáticas. Viajó por Egipto durante varios años y allí adquirió una sólida formación mística y religiosa. De vuelta a Samos fundó una sociedad religiosa y filosófica. Por razones políticas, abandona Grecia y se instala, con su escuela, en Crotona, al sur de Italia. La sociedad que fundó tenía un régimen muy estricto y un rígido código de conducta. Superado un período de prueba, se permitía a los iniciados en la secta oír al maestro, oculto tras una cortina. Años más tarde se les permitiría ver a Pitágoras directamente. Los pitagóricos creían que, merced a las matemáticas, su espíritu podría ascender a través de las esferas celestiales hacia un mundo mejor. Son
muchos los resultados matemáticos atribuidos a esta secta, pero entre ellos destaca el teorema de Pitágoras, el cual todos hemos estudiado en la geometría elemental. Como una consecuencia natural de este teorema, los pitagóricos descubren los números irracionales; por ejemplo, el número raíz de 2 existe, ya que es la longitud de la hipotenusa de un triángulo rectángulo isósceles de lado 1. El descubrimiento de estos nuevos números desestabilizó totalmente sus antiguas concepciones. Cuenta la leyenda que, en un principio, intentaron mantener oculta una verdad tan ingrata incluso que su descubridor, Hipaso de Metaponto, fue arrojado al mar durante un viaje. Quizás por primera vez en la historia de la ciencia, el pensamiento abstracto había conducido inexorablemente a una conclusión que reducía a añicos las creencias de todos. Muchas
fueron las suspicacias que levantaron el carácter secreto de la sociedad pitagórica y sus rituales místicos, que se decía había importado de Egipto. Hacia el año 500 aC, Pitágoras se vio obligado a huir a Tarento y después a Metaponto, donde fue asesinado. Sus seguidores continuaron sus enseñanzas en diversos lugares aproximadamente durante un siglo. Los
pitagóricos estaban convencidos de que la clave para la comprensión del orden del universo se encerraba en los números, que para ellos se reducían al conjunto de los enteros positivos. Pitágoras había descubierto una notable relación entre los números y la música. Al pulsar la cuerda tensa de una guitarra se emite un sonido musical y la altura de la nota producida depende de la longitud de la cuerda pulsada. La sorprendente aportación de Pitágoras consistió en relacionar los tonos de los sonidos con razones de números enteros. Los pitagóricos llegaron a la conclusión de que todas las relaciones de la naturaleza eran expresables mediante relaciones de números. Tras
la disolución de la escuela pitagórica, muchas otras escuelas continuaron el estudio de la geometría. Uno de los principios de las matemáticas -y posiblemente de la mente humana- consiste en construir estructuras cada vez más complejas a partir de estructuras simples. Los griegos concibieron así curvas más complicadas a partir de la recta y de la circunferencia, tales como la cicloide, la epicicloide o la hipocidoide. Analizando las distintas formas de tomar la intersección de un plano con un cono, construyeron las secciones cónicas. Los principales resultados relativos a secciones cónicas fueron descubiertos por Apolonio de Pérgamo (262-190 aC) y están descritos en sus ocho libros, Secciones cónícas. Los cuatro primeros libros eran una revisión de trabajos debidos a Euclides que se han perdido para siempre. El descubrimiento de las secciones cónicas se atribuye a un discípulo de Platón, cuya escuela floreció durante el siglo IV aC en la ciudad estado de Atenas. |
Platón, discípulo de Sócrates, fundó su escuela, la Academia, en una zona sagrada de Atenas llamada Hekademeíe. La escuela de Platón era como una pequeña universidad donde el filósofo y sus amigos impartían enseñanzas a sus discípulos. Dos de los más grandes matemáticos de la antigüedad, Eudoxo de Cnidos (408-355 aC ) y Teateto (420-367 aC), fueron miembros de esta Academia. Aunque Platón no era matemático, tenía las matemáticas en tan alta estima que exigía a sus alumnos que dedicasen diez años de su vida a su estudio y cinco más a la filosofía. Dice la leyenda que la inscripción grabada en la entrada de la Academia rezaba: "No entre aquí quien no sepa geometría.". Para Platón la única matemática que debía ser objeto de estudio era aquella que se propusiera «elevar el conocimiento del alma hasta el conocimiento del bien una ciencia de la cual ningún arte ni ningún conocimiento pudiera prescindir.» La
otra matemática, la de los «mercaderes y traficantes que la cultivan con la vista puesta en las compras y las ventas» era considerada como una herramienta para los trabajos manuales, ajena a los centros académicos y a la filosofía. Estos dos aspectos conocidos actualmente como matemática pura y matemátíca aplicada, estuvieron bien delimitados en los primeros tiempos, pero más tarde se fueron interrelacionando y sus fronteras se volvieron cada vez más borrosas, hasta el momento actual, en el que las matemáticas forman una unidad. Se
dice que Platón propuso a sus discípulos explicar el movimiento de los cuerpos celestes mediante una combinación de diversos movimientos circulares y esféricos. Consideraba a la astronomía un simple juego de los geómetras, para quienes era fuente de interesantes problemas. Los griegos conocían los irregulares movimientos del Sol y de los planetas, aunque no podían explicarlos de una manera sencilla. Apolonio propuso que las órbitas celestes deberían ser descritas mediante la combinación de movimientos circulares. Del desarrollo de esta teoría se encargó Hiparco, el más grande astrónomo de la antigüedad. Su obra nos es conocida merced a la célebre colección Matemática escrita por Ptolomeo en la que se completaba el sistema ptolemeico o geocéntrico. No
es sorprendente que los astrónomos griegos situaran en el centro de nuestro universo a la Tierra y no al Sol, ya que lo que nosotros observamos es el movimiento del Sol alrededor de nuestro planeta. Sin embargo, ya en el siglo II antes de Cristo, Aristarco enseñaba que la Tierra y los demás planetas describían órbitas circulares en torno a un Sol fijo; esto es, el sistema heliocéntrico. Fueron varias las razones por las que sus hipótesis no fueron aceptadas. Entre otras, cabe señalar que los griegos no sabían y, en consecuencia, no podían explicar, cómo los objetos podían permanecer estables sobre la Tierra si ésta se movía, y porqué las nubes no quedaban rezagadas. Estos mismos argumentos volverían a ser utilizados casi dos mil años mas tarde cuando Copérnico propuso de nuevo la teoría del heliocentrismo. El
gusto exclusivo de Platón por las matemáticas puras perjudicó, sin duda, a las matemáticas aplicadas o prácticas. También debemos tener en cuenta que en esa época no se disponía de un sistema de numeración y cálculo manejable, ni de aparatos de observación y precisión con suficiente sensibilidad. Casi con seguridad, en el caso de que Platón y sus discípulos dispusiesen de ellos, se hubieran interesado por aplicaciones prácticas que de este modo les pasaron inadvertidas. Los
cinco sólidos platónicos representan la composición y armonía de las cosas. En el Timeo se dice que la Tierra está formada por átomos agrupados en forma de hexaedros; el fuego, de tetraedros, el aire, de octaedros, y el agua, de icosaedros. El universo en su totalidad está figurado en el dodecaedro. |
Ptolomeo |
 Es poco lo que se sabe de Claudio Ptolomeo: que era un sabio nacido en Egipto, que vivió en el siglo II dC en Alejandría y que su principal mérito fue reunir las observaciones astronómicas anteriores a él. De hecho fue el más grande divulgador científico de su época. Realizó observaciones y trabajos astronómicos entre los años 127 y 151. Escribió un tratado llamado Gran sintaxis matemática o Almagesto en el que sistematizó la astronomía antigua. El Almagesto constituye la primera sistematización de la hoy llamada «trigonometría plana y esférica». Construyó una tabla de cuerdas partiendo del valor de la cuerda de 1°, y mediante una utilización adecuada de las fórmulas del seno de la suma, Ptolomeo completó dicha tabla sirviéndole de control los valores ya calculados de cuerdas de arcos conocidos. Para las fracciones menores de 30º utilizó la interpolación lineal.Creía
que el Sol, la Luna y los planetas giraban en torno a la Tierra. A pesar de todo, su concepción del sistema solar se mantuvo durante catorce siglos. Pese a que el punto de partida del sistema tolemaico era equivocado, sus observaciones permitían conocer con relativa antelación y exactitud la posición de los planetas. Ptolomeo
realizó también un catálogo de estrellas (en el que recoge 1.028). Además describió con detalle los instrumentos que debían utilizarse en las observaciones astronómicas y redactó una Geografía basada en las informaciones que enviaban las legiones romanas que recorrían el mundo. |
George Polya definió en cierta ocasión la elegancia de los teoremas geométricos como "directamente proporcional al número de ideas que en ellos vemos, e inversamente proporcional al esfuerzo requerido para comprenderlas". |
Puig Adam |
Pedro Puig Adam (1900-1969) ha sido uno de los más importantes matemáticos españoles del presente siglo. Desarrolló una intensa labor en el campo de la didáctica de la matemática junto con Julio Rey Pastor. En 1926 obtiene la cátedra de matemáticas del Instituto San Isidro de Madrid, donde impartió su saber y su humanidad a muchas generaciones. Solía aconsejar a sus alumnos como norma de vida: «Tended a ser un poco aprendices de todo para vuestro bien y, al menos, maestros en algo para bien de los demás». Autor de numerosas publicaciones, entre las que cabe destacar su Geometría métrica, que ha sido y sigue siendo importante manual de estudio para muchas generaciones. Alcanzó los más importantes títulos de su época: doctor, ingeniero, académico, Gran Cruz de Alfonso X el Sabio, comendador de la Orden del Mérito Civil, etcétera, pero, con toda seguridad, el título más importante que alcanzó fue el cariño, respeto y admiración de todos sus alumnos, entre los que cabe destacar al actual rey de España D. Juan Carlos I que siendo niño fue instruido en su residencia de Las Jarillas por don Pedro. Una
frase suya: "Aprended a ser un poco aprendices de todo para vuestro bien y, al menos, especialistas en algo para bien de los demás." |
En las laderas del monte Rushmore, en Dakota del Sur (EE.UU.) están esculpidos los rostros de cuatro presidentes norteamericanos. Para trasladar a la roca los rasgos de los presidentes, el escultor Gutzon Borglum hizo primero unos bustos a un doceavo del tamaño que tendrían los definitivos. En el centro de la cabeza de esas maquetas colocó un brazo giratorio del que pendía un hilo con una plomada. Ese peso podía moverse arriba y abajo y adelante y atrás a lo largo del brazo. Éste a su vez podía girar y registrar en cada momento su ángulo gracias a un transportador. Un brazo semejante pero mucho mayor (10 metros) fue colocado en el centro de lo que iba a ser la cabeza tallada en la roca. Para saber, por ejemplo, dónde había que situar la punta de la nariz, bastaba marcarlo con la plomada en la maqueta y luego trasladar las medidas, multiplicadas por 12, a la roca.